Introduction

The leidenalg package facilitates community detection of networks and builds on the package igraph. We abbreviate the leidenalg package as la and the igraph package as ig in all Python code throughout this documentation. Although the options in the leidenalg community detection package are extensive, most people are presumably simply interested in detecting communities with a robust method that works well. This introduction explains how to do that.

For those without patience (and some prior experience), if you simply want to detect communities given a graph G using modularity, you simply use

>>> partition = la.find_partition(G, la.ModularityVertexPartition);

That’s it.

The result partition is in this case a ModularityVertexPartition which is derived from the igraph type ig.VertexClustering, see the documentation for more details.

Why then should you use this package rather than for example the Louvain algorithm community_multilevel() built into igraph? If you want to use modularity, and you work with a simple undirected, unweighted graph, then indeed you may use the built-in method. For anything else, the functionality is not built-in and this package is for you. Moreover, the Leiden algorithm is typically faster than the Louvain algorithm and returns partitions of a higher quality.

For those less familiar with igraph, let us work out an example more fully. First, we need to import the relevant packages:

>>> import igraph as ig
>>> import leidenalg as la

Let us then look at one of the most famous examples of network science: the Zachary karate club (it even has a prize named after it):

>>> G = ig.Graph.Famous('Zachary')

Now detecting communities with modularity is straightforward, as demonstrated earlier:

>>> partition = la.find_partition(G, la.ModularityVertexPartition)

You can simply plot the results as follows:

>>> ig.plot(partition) 

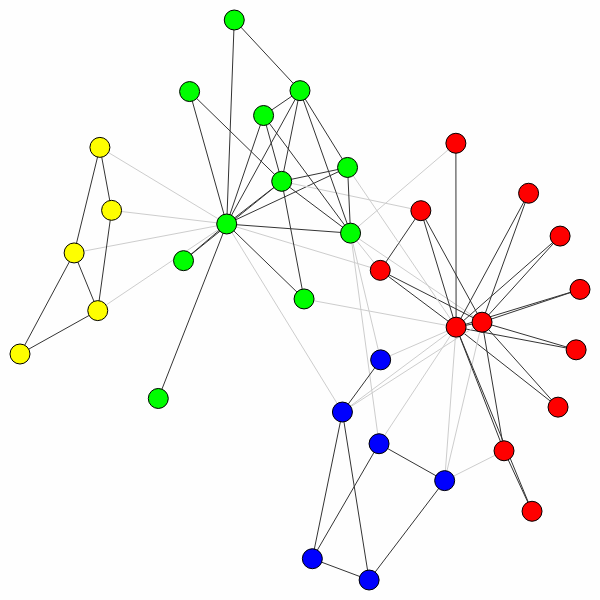
In this case, the algorithm actually finds the optimal partition (for small graphs like these you can check this using community_optimal_modularity() in the igraph package), but this is generally not the case (although the algorithm should do well). Although this is the optimal partition, it does not correspond to the split in two factions that was observed for this particular network. We can uncover that split in two using a different method, CPMVertexPartition:

>>> partition = la.find_partition(G, la.CPMVertexPartition,
...                                    resolution_parameter = 0.05);
>>> ig.plot(partition) 

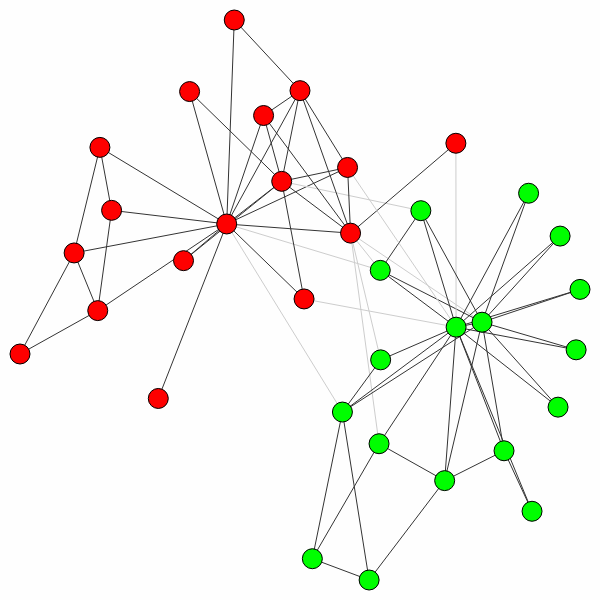
Note that any additional **kwargs passed to find_partition() is passed on to the constructor of the given partition_type. In this case, we can pass the resolution_parameter, but we could also pass weights or node_sizes.

This is the real benefit of using this package: it provides implementations for six different methods (see Reference), and works also on directed and weighted graphs. In addition, it also provides flexible functionality for customizing to some extent the optimisation routines (see Advanced). Finally, it also allows to work with more complex multiplex graphs (see Multiplex).

The Leiden algorithm [1] extends the Louvain algorithm [2], which is widely seen as one of the best algorithms for detecting communities. However, the Louvain algorithm can lead to arbitrarily badly connected communities, whereas the Leiden algorithm guarantees communities are well-connected. In fact, it converges towards a partition in which all subsets of all communities are locally optimally assigned. Finally, the Leiden algorithm is also much faster, because it relies on a fast local move routine. The “canonical” Leiden algorithm is implemented in Java and is faster than this implementation, but less extensive.

References

1

Traag, V.A., Waltman. L., Van Eck, N.-J. (2018). From Louvain to Leiden: guaranteeing well-connected communities. arXiv:1810.08473

2

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 10008(10), 6. 10.1088/1742-5468/2008/10/P10008